Lab 3: Linear models with one categorical predictor-- t-tests • FANR6750

Lab 2

Introduction to RMarkdown
Introduction to RProjects and directories
Submitting HWs

Today’s topics

Introduction
Linear models with one categorical predictor: t-tests
- One sample
- Samples vs tails
- Two sample
- Graphics Review
- Paired

Introduction

Today we will discuss a range of scenarios which broadly fall under the category of t-tests. These will include:

when a sample mean is being compared to a particular value (one-sample t-test)
when two sample means are being compared to each other and the observations between samples are independent (two-sample t-test)
when two sample means are being compared to each other and the observations between samples are paired (paired t-test)

Scenario 1: One sample t-tests

For now, we will talk about the scenario in which we only have one sample of data and we are interested in its mean.
Question: Is the average height of students at UGA equal to 65 inches?
Problem: We don’t know the true population mean (\(\mu_1\)). All we have is the sample mean (\(\bar{y}_1\)).
The relevant hypotheses are:
- \(H_0 : \mu_1 = 65\)
- \(H_A : \mu_1 \neq 65\)

Suppose we have collected a random sample of 100 students. Below is a plot of the distribution of their heights. In this case the sample mean is 61 inches. From the plot below, it would be difficult to conclude one way or another whether the population mean is equal to 65.

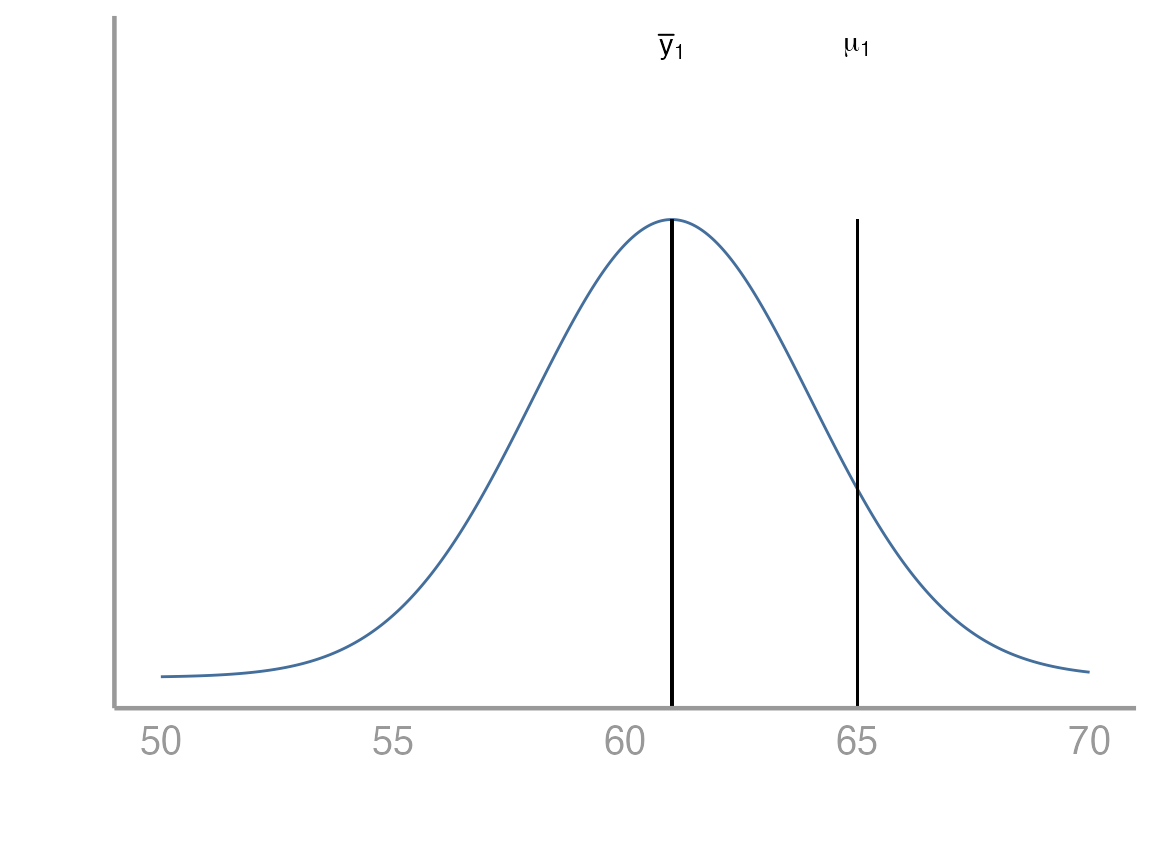
We can think about this problem in a few different ways. Below we will see how to approach it both from the perspective of a linear model as well as from the perspective of a test. Remember that in our linear model below we are interested in estimating \(\beta_0\) which in this very simple case just represents the population mean.

\[ y_i = \beta_0 + \epsilon_i \ \ \ \ \ \text{where} \ \ \ \ \ \epsilon_i \sim \text{N}(0,\sigma) \]

Key points

If the sample mean (\(\bar{y}_1\)) is very different from the proposed population mean and the standard error of the difference is small, the \(t\)-statistic will be far from zero
If the \(t\)-statistic is more extreme than the critical values, we reject the null hypothesis (\(H_0\))

Exercise 1

Formulation as a linear model

Open your FANR6750 RStudio project (if you have one)
Create a new R script and save it to the directory where you store you lab activities. Name it something like lab04-t_tests.R
Load the FANR6750 package and the studentsdata object

library(FANR6750)
data("studentsdata")

Create an object students which is the vector in the studentsdata dataframe.

students <- studentsdata$students

Fit a linear model to this dataset.

mod1 <- lm(students - 65 ~ 1)
summary(mod1)
#> 
#> Call:
#> lm(formula = students - 65 ~ 1)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -10.406  -2.181  -0.156   1.819   7.794 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)   -3.594      0.321   -11.2   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 3.21 on 99 degrees of freedom

A few things to think about here:

Why did we include the - 65 in the model statement?
What does the ~ 1 represent?
What does the intercept value mean?
What do we conclude from this model and p-value?

Formulation as a t-test by hand

Now that we have seen how R can create a linear model to help us answer the question about the population mean, we will dive deeper into what exactly the computer is doing. How exactly did it decide to reject the null hypothesis? How did it calculate the p-value? Where did it get those numbers?

We know from lecture that the formula to get a test statistic for a one sample test is the following:

\[ t = \frac{\bar{y} - \mu_0}{SEM} \ \ \ \ \ \text{where} \ \ \ \ \ SEM = \frac{s}{\sqrt{n}} = \frac{\sqrt{\frac{1}{n-1}\sum^n_{i=1}(y_i - \bar{y})^2}}{\sqrt{n}} \] While this looks like a lot, we can break it into pieces as lines of code in R.

Create an object which is the sample mean.

y_bar <- mean(students)

Create an object which is the standard error

se_y <- sd(students)/sqrt(length(students))

Put these together to calculate the test statistic

t_stat <- (y_bar - 65)/se_y

Now that we have a test statistic, we need to calculate a critical value for comparison.

Calculate the critical values

alpha <- 0.05
t_crit <- qt(c(alpha/2, 1-alpha/2), df= length(students)-1)

Notice that the results are the same as when we used the lm() function.

Formulation as a t-test using the built in R function

Use the built in R function t.test().

t.test(students, mu= 65, alternative= 'two.sided', conf.level= 0.95)
#> 
#>  One Sample t-test
#> 
#> data:  students
#> t = -11, df = 99, p-value <2e-16
#> alternative hypothesis: true mean is not equal to 65
#> 95 percent confidence interval:
#>  60.77 62.04
#> sample estimates:
#> mean of x 
#>     61.41

Samples vs Tails

Before we go any further, lets address an issue that many students find confusing about t-tests. This is the issue of samples vs tails. What does it mean when we talk about a ‘one sample t-test vs a two sample t-test’? What does it mean when we say a t-test had ‘one tail or two tails’?

Samples: The number of samples (one or two) has to do with the data that you are using to approach the research question. If you are comparing one sample to a specific value (e.g. \(\mu_1 = 6\)) we call that a one sample test. If instead, you are comparing two sample means to eachother, we call that a two sample test
Tails: The number of tails (one or two) is related to the specific research question that you are interested in asking and it is directly informed by the null and alternative hypotheses. A two tailed test will have hypotheses like those below:

\[ H_0: \mu_1 = x \]

\[ H_A: \mu_1 \ne x \]

Notice the \(=\) and \(\ne\) in the hypotheses. \(\mu_1\) may be being compared to a specific value or being compared to another mean (e.g. \(\mu_2\)) but the hypotheses are always set up as \(=\) vs \(\ne\).

In constrast, a one tailed test will have hypotheses like these below:

\[ H_0: \mu_1 \le x \]

\[ H_A: \mu_1 > x \]

Or the other way around:

\[ H_0: \mu_1 \ge x \]

\[ H_A: \mu_1 < x \]

Notice that in a one tailed test, the alternative is only interested in one direction and the null includes everything else.

In what types of situations might you want to set up a t-test as one tailed? What about two tailed? Which do you think has more statistical power to detect an effect?

Scenario 2: Two sample t-tests

In this dataset, we have the average number of calls over 10 minutes during point count surveys for Song Thrushes (Turdus philomelos), a species of song bird in eastern Europe. The researcher is interested in understanding how wind may be affecting the frequency of bird calls. Specifically, she would like to know whether high wind conditions results in fewer average calls over 10 minutes than low wind conditions.
Question: Do the samples come from the same population, or do they come from populations with different means?
Problem: We don’t know the true population means (\(\mu_H\), \(\mu_L\))
Under the assumption that the variances of the two populations are equal, the relevant hypotheses are:
- \(H_0 : \mu_H \ge \mu_L\)
- \(H_A : \mu_H < \mu_L\)

How many tails are in this test? Why did we decide to do that?

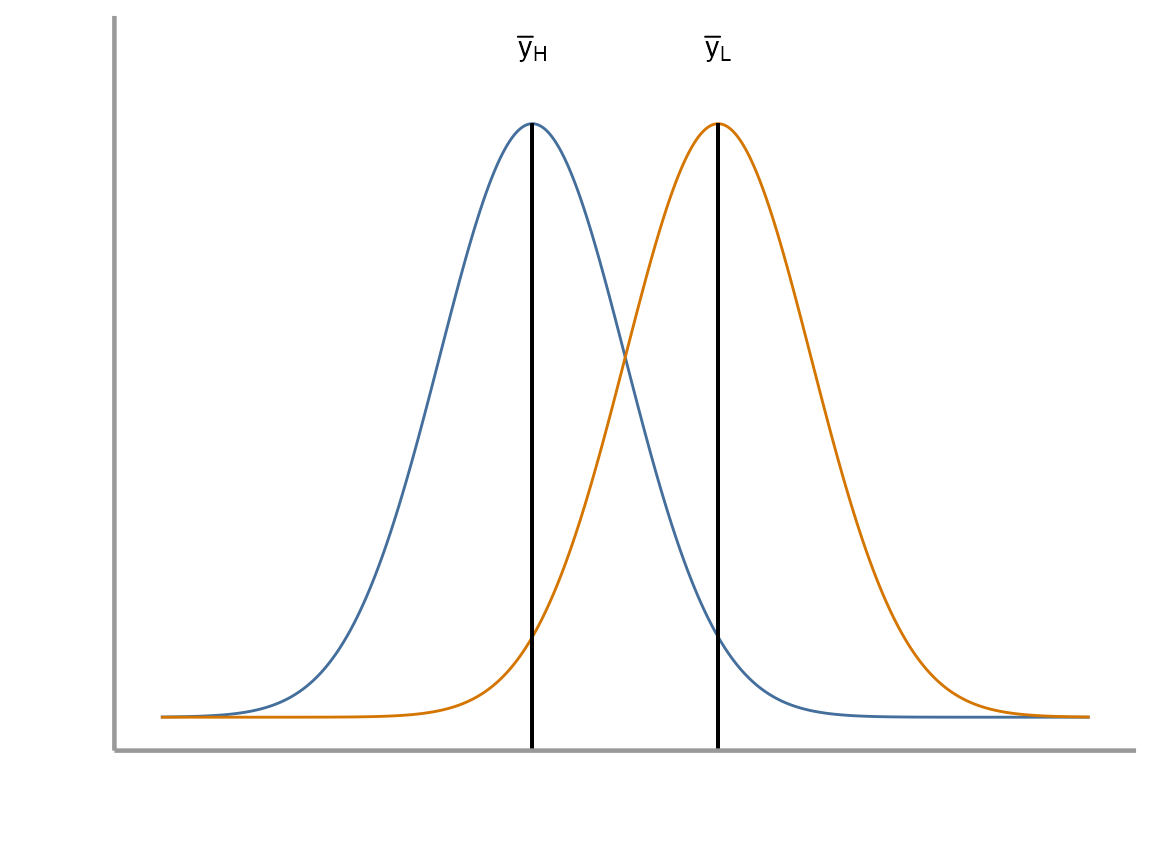
We will again see how this problem can be approached from the perspective of a linear model as well as being considered as a test. Below is the linear model for the two sample t-test. It should look similar to the last one we used, but now we have added the complexity of two categorical levels (i.e. high wind vs low wind):

\[ y_i = \beta_0 + \beta_1x_i + \epsilon_i \ \ \ \ \ \text{where} \ \ \ \ \ \epsilon_i \sim \text{N}(0,\sigma) \]

How do we interpret \(\beta_0\) and \(\beta_1\)?

Exercise 2

Formulation as a linear model

Load the FANR6750 package and the thrushdata object. Lets look at the structure and summary of the dataset as well

library(FANR6750)
data("thrushdata")

str(thrushdata)
#> 'data.frame':    100 obs. of  2 variables:
#>  $ calls: num  9.1 5.7 7.7 14.9 12.3 16.7 17.8 11.6 7.5 14.3 ...
#>  $ wind : chr  "high" "high" "high" "high" ...
summary(thrushdata)
#>      calls          wind          
#>  Min.   : 5.7   Length:100        
#>  1st Qu.:11.3   Class :character  
#>  Median :14.1   Mode  :character  
#>  Mean   :14.1                     
#>  3rd Qu.:16.7                     
#>  Max.   :23.4

# Notice from the str() and summary() functions that R is interpreting the 'wind' variable 
# as a character. Because we would like to treat 'wind' as a grouping variable, we can 
# convert it to a factor in R.

thrushdata$wind <- as.factor(thrushdata$wind)

Fit a linear model to the data which estimates call frequency as a function of wind conditions.

mod2 <- lm(calls~ wind, data= thrushdata)
summary(mod2)
#> 
#> Call:
#> lm(formula = calls ~ wind, data = thrushdata)
#> 
#> Residuals:
#>    Min     1Q Median     3Q    Max 
#>  -6.02  -2.42  -0.12   2.17   6.95 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)   11.720      0.414   28.32  < 2e-16 ***
#> windlow        4.730      0.585    8.08  1.7e-12 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 2.93 on 98 degrees of freedom
#> Multiple R-squared:   0.4,   Adjusted R-squared:  0.394 
#> F-statistic: 65.3 on 1 and 98 DF,  p-value: 1.69e-12

How would you interpret these results? Is there a difference in call frequency as a function of wind conditions? Which of these numbers represent \(\beta_0\) and \(\beta_1\) in our linear model above?

Formulation as a t-test by hand

Similar to Exercise 1, we could calculate a test statistic by hand. The formulas for creating this test statistic as well as the pooled variance are shown below:

\[\large t = \frac{(\bar{y}_H − \bar{y}_L) − (\mu_H − \mu_L)}{\sqrt{s^2_p/n_H + s^2_p/n_L}}\]

where \(s^2_p\) is the pooled variance

\[\large s^2_p = \frac{(n_H − 1)s^2_H + (n_L − 1)s^2_L}{n_H + n_L − 2}\]

We will leave it as an exercise for you to perform. The general steps are as follows:

Calculate the test statistic by defining all the necessary terms in R
Calculate the appropriate critical value/values
Compare the test statistic to the critical value/values and reach a conclusion about the hypotheses in question

Formulation as a t-test using the built in R function

Create two objects which represent the calls vectors for high and low wind conditions

yL <- thrushdata$calls[thrushdata$wind== 'low']
yH <- thrushdata$calls[thrushdata$wind== 'high']

Use the t.test() function to perform the two sample t-test

t.test(yH, yL, var.equal = TRUE, paired = FALSE, alternative = "less")
#> 
#>  Two Sample t-test
#> 
#> data:  yH and yL
#> t = -8.1, df = 98, p-value = 8e-13
#> alternative hypothesis: true difference in means is less than 0
#> 95 percent confidence interval:
#>    -Inf -3.758
#> sample estimates:
#> mean of x mean of y 
#>     11.72     16.45

Make sure you set var.equal=TRUE. Otherwise, R will assume that the variances of the two populations are unequal. We can test this assumption using the code below.

var.test(yH, yL)
#> 
#>  F test to compare two variances
#> 
#> data:  yH and yL
#> F = 1.2, num df = 49, denom df = 49, p-value = 0.5
#> alternative hypothesis: true ratio of variances is not equal to 1
#> 95 percent confidence interval:
#>  0.6874 2.1345
#> sample estimates:
#> ratio of variances 
#>              1.211

What do we conclude? Was it appropriate for us to assume equality of variances? What could we have done if this assumption was not met?

We can also formulate our t-test using some different syntax. It will give us exactly the same results though.

t.test(calls ~ wind, data = thrushdata, 
       var.equal = TRUE, paired = FALSE, 
       alternative = "less")
#> 
#>  Two Sample t-test
#> 
#> data:  calls by wind
#> t = -8.1, df = 98, p-value = 8e-13
#> alternative hypothesis: true difference in means is less than 0
#> 95 percent confidence interval:
#>    -Inf -3.758
#> sample estimates:
#> mean in group high  mean in group low 
#>              11.72              16.45

We have performed the t-test for this dataset but it would be nice if we could plot the data. This section below provides a brief introduction to plotting in R.

Graphics

R has very powerful graphing capabilities that make it possible to create data visualizations for reports or publications. As with most tasks in R, there are many ways to create graphs and you will find that people have very strong feelings about the best approach.

The debate over graphics in R usually boils down to using the built-in graphing functions (“base graphics”) vs the ggplot2 package. There are some advantages to both approaches, but for the most part the newer generations of R users prefer ggplot2. Therefore most of the sample code provided in lab will reflect that preference. However, I don’t care how you make your plots as long as they effectively display the information you are trying to convey. If you prefer base graphics, by all means use base graphics.¹

Brief introduction to `ggplot2`

Because the code I provide will use ggplot2, it is worth briefly learning/reviewing how this package approaches data visualization.

The power and flexibility of ggplot2 come from it’s consistent structure. Although a bit confusing at first, once you get the hang of it, the structure actually makes it quite easy to create highly customized visualizations. All plots created using ggplot2 use the same underlying structure:

\[\underbrace{ggplot}_{initiate\; plot}(\underbrace{data = df}_{data\;frame},\; \underbrace{aes(x =\; , y = \;)}_{plot\; attributes}) + \underbrace{geom\_line()}_{geometry}\]

The ggplot() function initiates a new plot. In this function, you tell ggplot2 what data frame you will be using for the plot (ggplot only accepts data frames as input) and you tell it how to map attributes of the data to the visual properties of the figures. Attributes are mapped inside the aes() argument. Attributes usually include location (x-axis and y-axis placement), color, size, shape, line type, and many others. In general, each attribute will be mapped to one column of your data frame.

The ggplot() function simply initiates a graph - if you run just that portion of the code you will get a blank graph. We can see that by creating a new plot showing the relationship between wind (the x-axis of the plot) and calls (the y-axis):

ggplot(data = thrushdata, aes(x = wind, y = calls))

You can see that ggplot created a figure with the correct axes and labels. But no data. That’s because we didn’t tell ggplot what type of geometry to use to represent the data. Once we add a geometry, we can see the data:

ggplot(data = thrushdata, aes(x = wind, y = calls)) + 
  geom_point()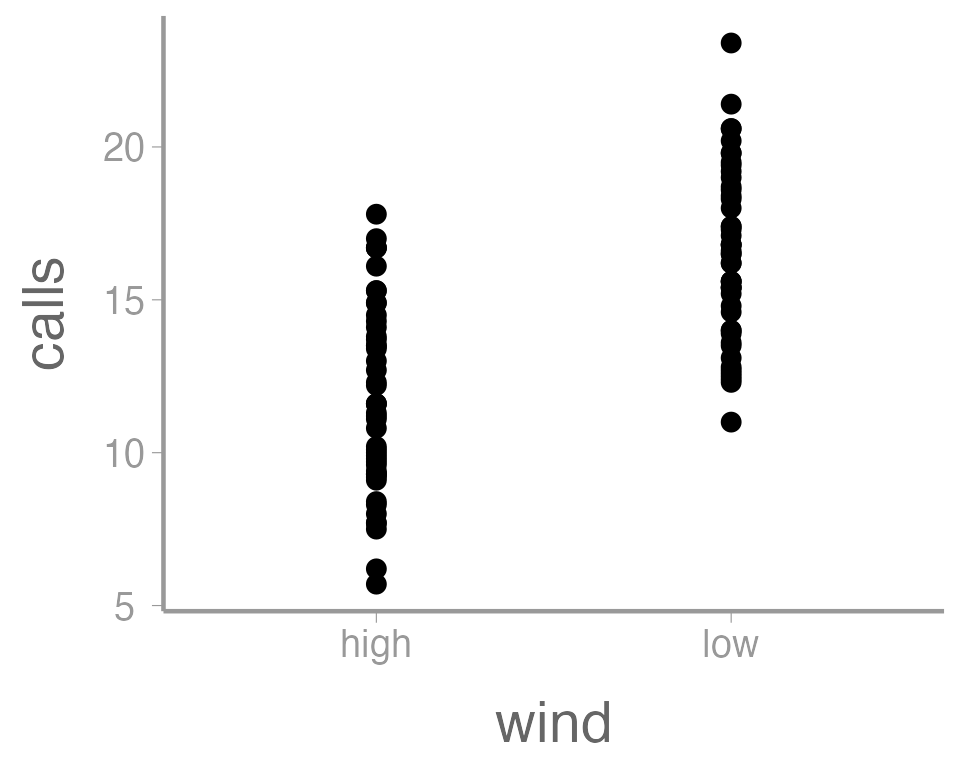

In this case, a boxplot might make more sense:

ggplot(data = thrushdata, aes(x = wind, y = calls)) + 
  geom_boxplot()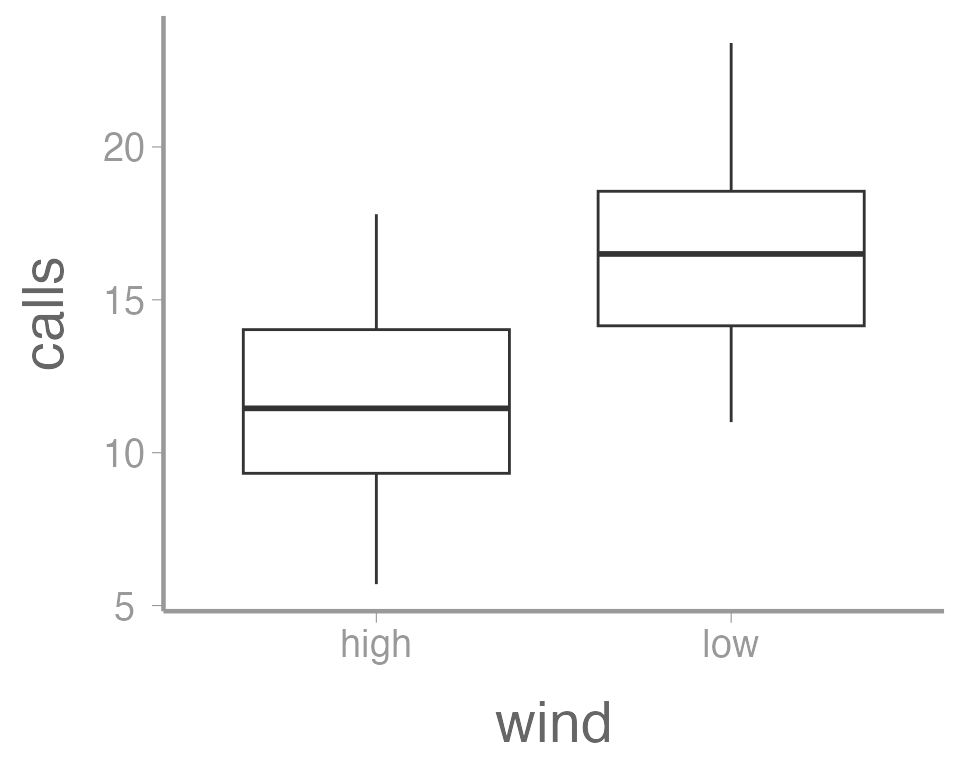

It’s also possible to use more than one geometry:

ggplot(data = thrushdata, aes(x = wind, y = calls)) + 
  geom_boxplot() +
  geom_point()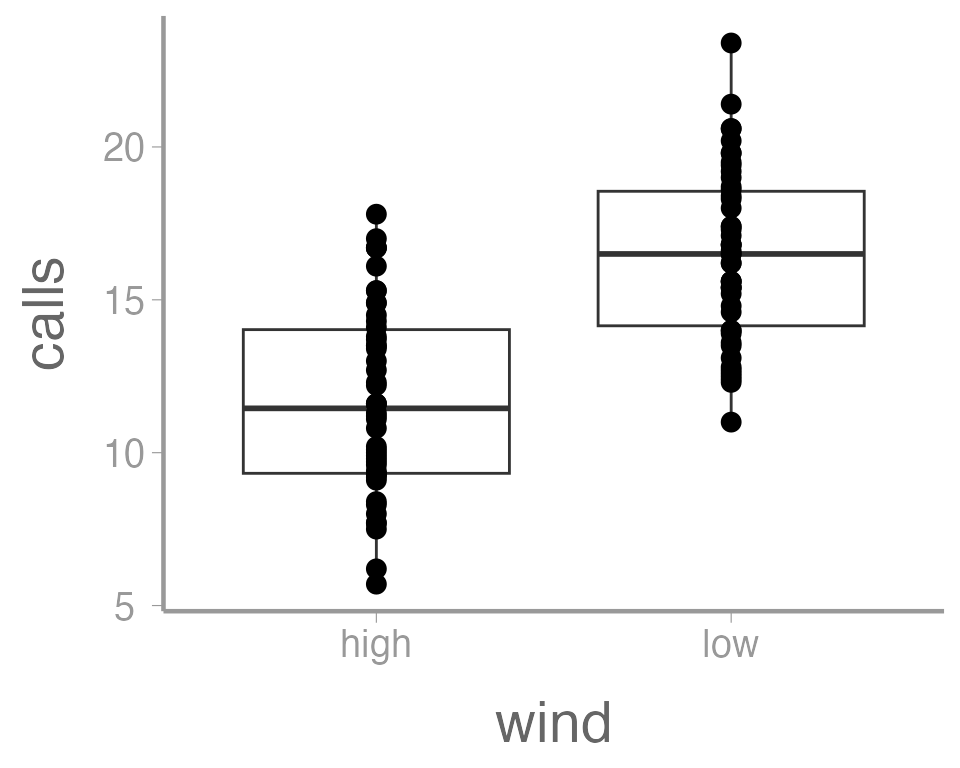

This is reasonable figure showing call frequencies as a function of wind. But ggplot2 makes it very easy to tweak the way the data is visualized (maybe too easy, you can spend a lot of time tweaking minor details). For example, maybe we want to color the points based on the wind. Because we want to map an attribute (color) to a variable (wind), we make this change inside of aes:

ggplot(data = thrushdata, aes(x = wind, y = calls, color = wind)) + 
  geom_boxplot() +
  geom_point()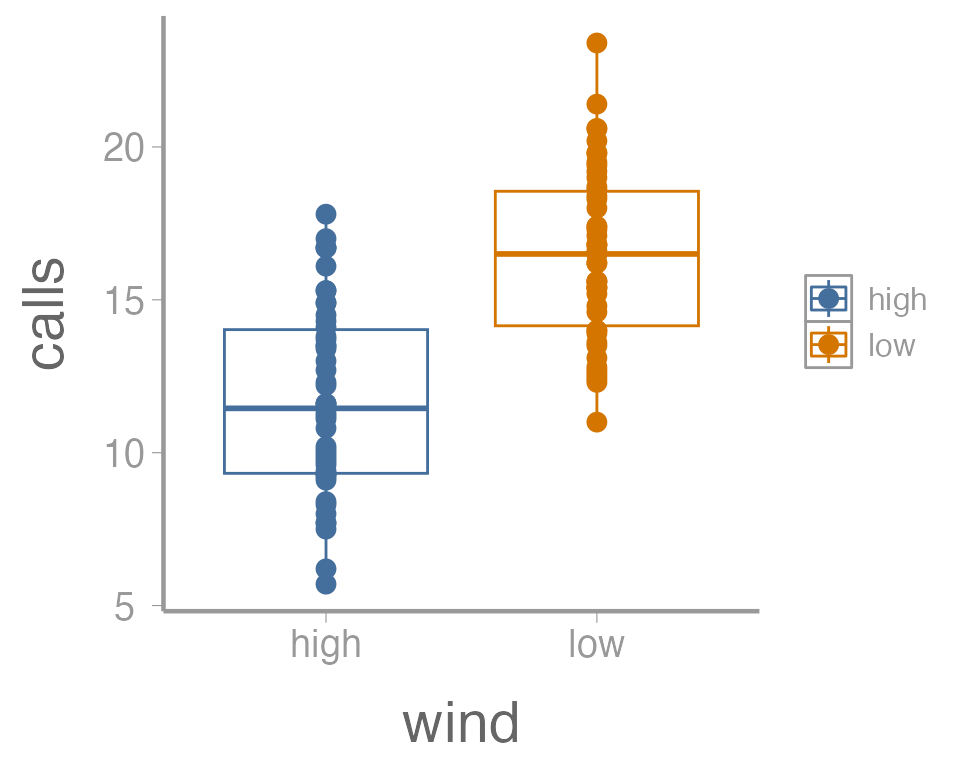

That’s not exactly what we wanted. Both the boxplot and the points now colored a function of wind. To make just the points a function of wind, we specify color = wind inside of the geom_point() function (anything in the ggplot() function will apply to all geoms):

ggplot(data = thrushdata, aes(x = wind, y = calls)) + 
  geom_boxplot() +
  geom_point(aes(color = wind))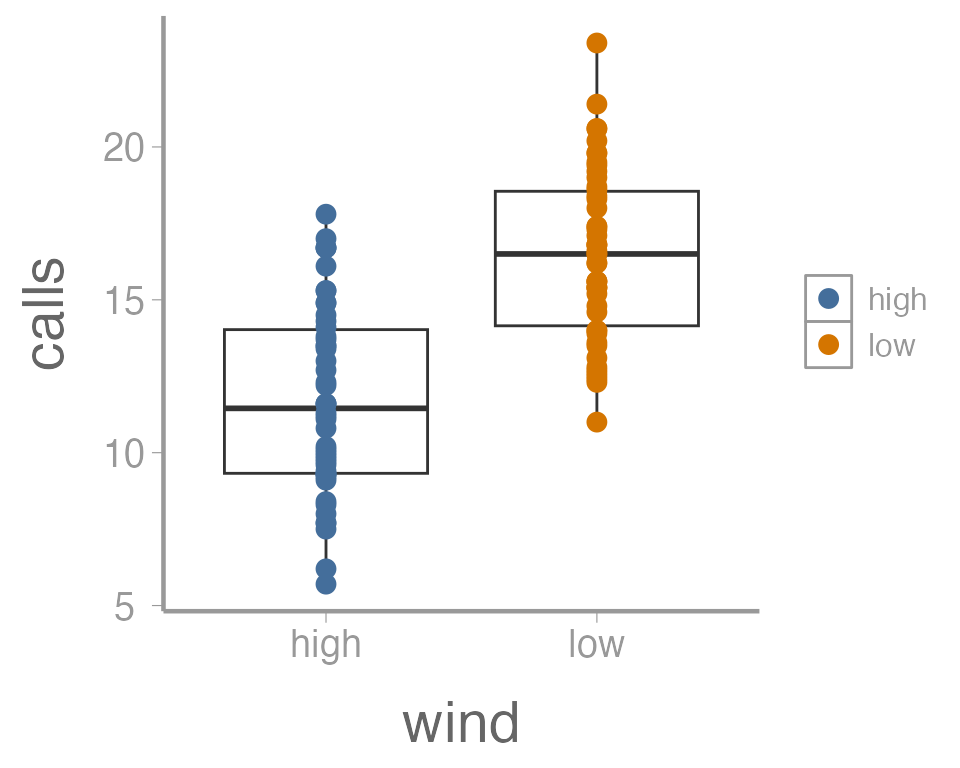

We can also do things like the change the size of the geometries. In this case, we are not mapping a variable to an attribute (size is not a function of the data values). So these changes happen outside of the aes() argument:

ggplot(data = thrushdata, aes(x = wind, y = calls)) + 
  geom_boxplot() +
  geom_point(aes(color = wind), size = 5)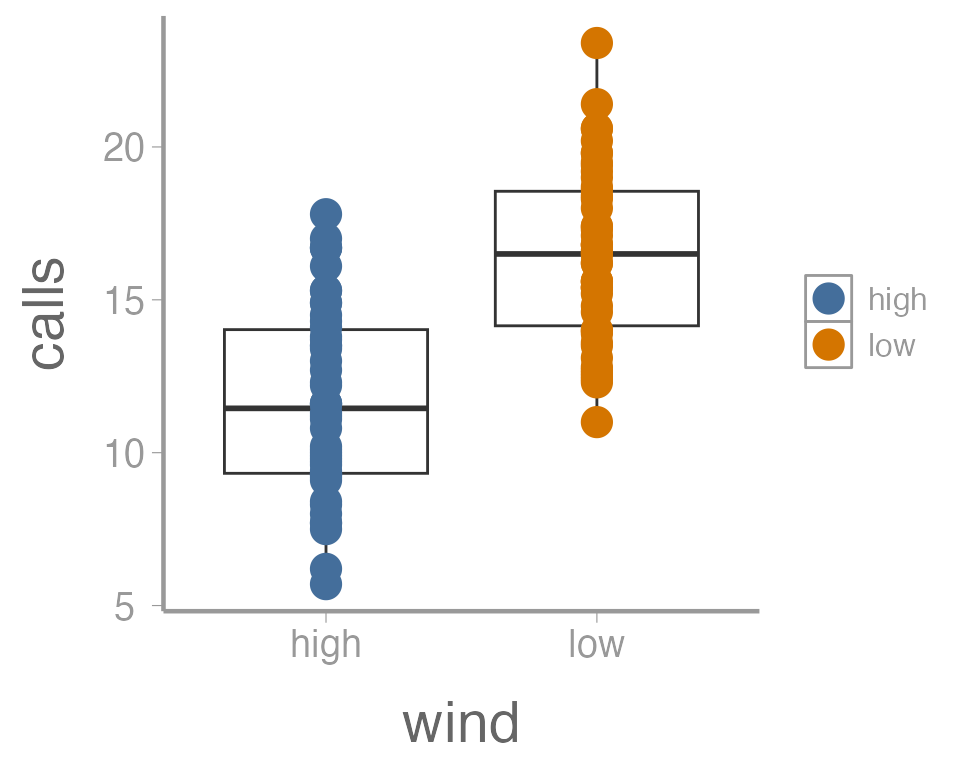

One last example. Because many of the points overlap, it can be hard to tell how many individual points there are in each group. One way to deal with overplotting like this is to make each point slightly transparent. We can do that with the alpha parameter:

ggplot(data = thrushdata, aes(x = wind, y = calls)) + 
  geom_boxplot() +
  geom_point(aes(color = wind), size = 5, alpha = 0.5)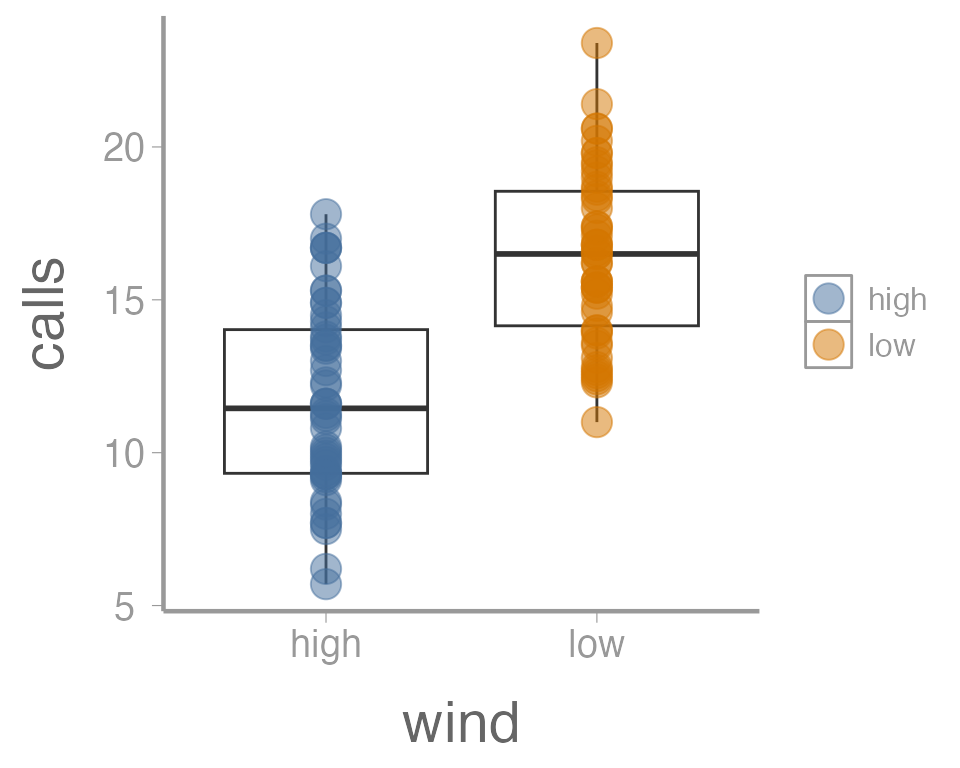

Again, because we aren’t mapping the alpha value to any data, we include it outside of aes().

Exercise 3

The graph above is fine for a quick visualization of the data but wouldn’t be appropriate for including in publications or reports. On your own,

Improve the axis labels. This could include: title case, units, font size, etc. Run ?scale_y_continuous and ?scale_x_discrete if you need some help (and note the difference between these two functions!). ?theme may also be useful
Manually change the color of the points (?scale_color_manual)
Instead of displaying the data using a boxplot, create histograms showing the distribution of call densities at each level of wind (?geom_histogram)

As you learn about graphics functions, whether base or ggplot2, you will probably need to look up help for how to do certain things. Google is usually your best bet but here are a few other good references:

The fantastic Fundamentals of Data Visualization book by Claus Wilke
The ggplot2 package website
And, yes, even the base R graph gallery

Scenario 3: Paired t-test

In this dataset, the researcher is interested in studying the effects of a pesticide on caterpillar populations. Twelve bushes are examined and the number of caterpillars on each bush is recorded. The pesticide is applied and after 3 days the number of caterpillars on each bush is recorded again.
Question: Does the pesticide have a negative effect on the caterpillar population?
Note: Paired t-tests can be thought of as a one sample t-test on the differences.
The hypotheses for this test would be the following:

\[ H_0: \mu_T \ge \mu_U \]

\[ H_A: \mu_T < \mu_U \]

Another way we could think about this is to say that \(\mu_U - \mu_T = \mu_D\). From here, we can formulate the hypotheses as:

\[ H_0: \mu_D \le 0 \]

\[ H_A: \mu_D > 0 \]

Exercise 4

Formulation as a linear model

In this case, we already know that the paired t-test can be thought of as a one sample t-test on the differences. As a result, the linear model can be set up in the same way as Scenario 1 above. This will be left as an exercise

Formulation as a t-test by hand

This will be left as an exercise for you but the general steps are as follows:

Load the caterpillar dataset

data("caterpillardata")

Calculate the difference between the untreated and treated values

caterpillardata$diff <- caterpillardata$untreated - caterpillardata$treated

mean(caterpillardata$diff)
#> [1] 1.5

Is the mean different from zero?

ggplot(data = caterpillardata, aes(y = diff)) + 
  geom_boxplot() +
  geom_hline(yintercept = 0, linetype = "dashed")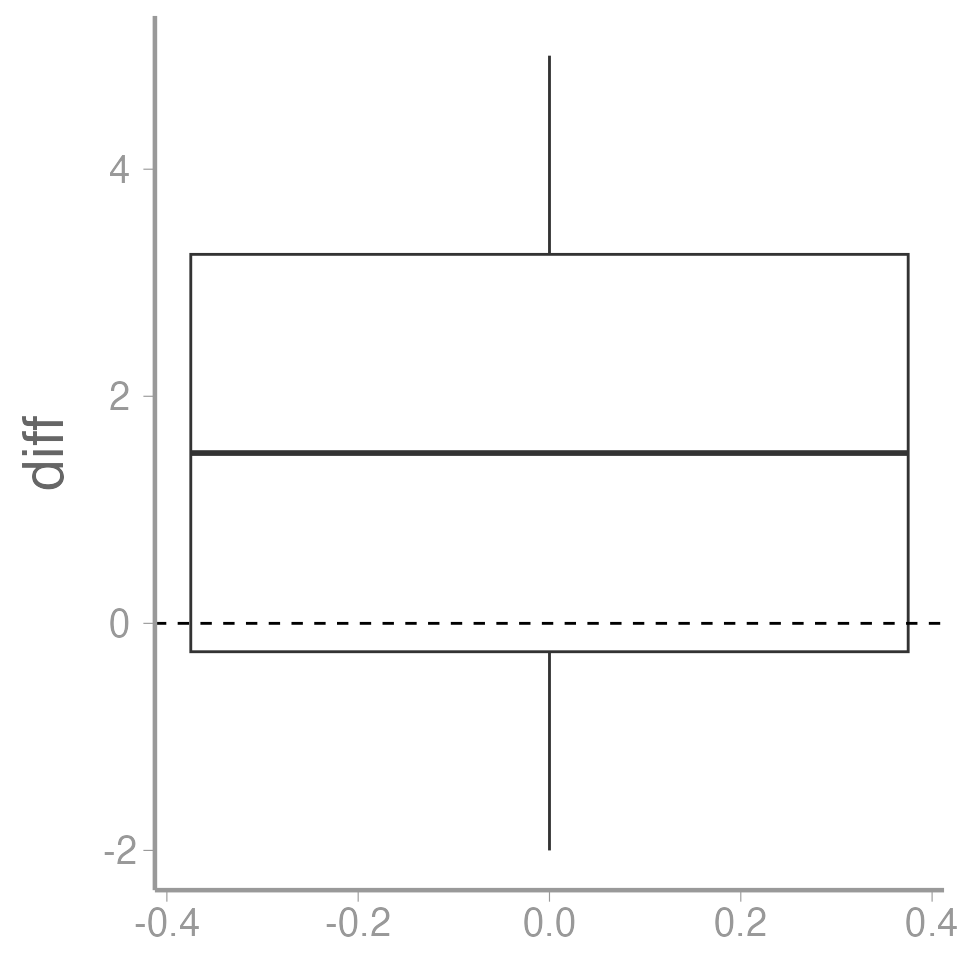

Calculate the standard deviation of the differences

\[\large s_d = \sqrt{\frac{1}{n-1}\sum_{i=1}^n(y_i - \bar{y})^2}\]

Calculate the test statistic

\[\large t = \frac{\bar{y}-0}{s_d/\sqrt{n}}\]

Compare to appropriate critical value and draw a conclusion

Formulation as a t-test using the built in R function

Use the t.test() function in R to perform the test

t.test(caterpillardata$diff, mu= 0, alternative= 'greater')
#> 
#>  One Sample t-test
#> 
#> data:  caterpillardata$diff
#> t = 2.3, df = 11, p-value = 0.02
#> alternative hypothesis: true mean is greater than 0
#> 95 percent confidence interval:
#>  0.3408    Inf
#> sample estimates:
#> mean of x 
#>       1.5

Excercise

This dataset comes from fisheries landings data for Yellowfin tuna (Thunnus albacares). The weight in pounds was recorded for each fish as well as presence of the larval form of a Lacistorhynchidae tapeworm (Dasyrhynchus talismani). The researcher believes that the presence of the tapeworm likely results in a less healthy and therefore lighter fish.

Create an R Markdown file to do the following:

Create an R chunk to load the tuna data using:

library(FANR6750)
data("tunadata")

Make a figure to show the weights of both infected and healthy tuna. You should spend some time considering what type of figure would best display this data (1 pt).
Create a header called “Hypotheses” and under this header, in plain English indicate what the null and alternative hypotheses are for the t-test. Also use R Markdown’s equation features to write these hypotheses using mathematical notation. In order to do this, you will need to consider what type of test would be appropriate for this data and how many tails the test will have (1 pt).
Create a header called “t-test by hand”. Under this header, do a t-test on the tuna data without using the t.test() function. Use only the functions mean, sd, and possibly length. Be sure to annotate your code (either within the R chunk using # or as plain text within the R Markdown file) and state the decision (reject or fail to reject the null) based on your results (2 pt).
Create a header called “t-test in R”. Under this header, do the t-test again, but this time using the t.test function (1 pt).
- Assume variances are equal
Add a section at the end of your file called “Discussion” and explain why you think the t-test failed to reject the null hypothesis even though the sample means were ~60 pounds different (almost a 20% difference in weight). What about the data may have caused this result? (1 pt)

A few things to remember when creating the document:

Be sure the output type is set to: output: html_document
Be sure to set echo = TRUE in all R chunks so that all code and output is visible in the knitted document
Regularly knit the document as you work to check for errors
See the R Markdown reference sheet for help with creating R chunks, equations, tables, etc.

Keep in mind that although we will be using ggplot2, it is a good idea to have some understanding of how base R graphics work. Most packages in R, when they produce some sort of output in the form of a plot, will still create that plot using base R graphics rather than ggplot. In order to alter those graphics without having to start from scratch, it will be useful to know a little about base R graphics.↩︎

Lab 3: Linear models with one categorical predictor– t-tests

FANR 6750: Experimental Methods in Forestry and Natural Resources Research

Fall 2024

Lab 2

Today’s topics

Introduction

Scenario 1: One sample t-tests

Key points

Exercise 1

Formulation as a linear model

Formulation as a t-test by hand

Formulation as a t-test using the built in R function

Samples vs Tails

Scenario 2: Two sample t-tests

Exercise 2

Formulation as a linear model

Formulation as a t-test by hand

Formulation as a t-test using the built in R function

Graphics

Brief introduction to `ggplot2`

Exercise 3

Scenario 3: Paired t-test

Exercise 4

Formulation as a linear model

Formulation as a t-test by hand

Formulation as a t-test using the built in R function

Excercise

Lab 3: Linear models with one categorical predictor– t-tests

FANR 6750: Experimental Methods in Forestry and Natural Resources Research

Fall 2024

Lab 2

Today’s topics

Introduction

Scenario 1: One sample t-tests

Key points

Exercise 1

Formulation as a linear model

Formulation as a t-test by hand

Formulation as a t-test using the built in R function

Samples vs Tails

Scenario 2: Two sample t-tests

Exercise 2

Formulation as a linear model

Formulation as a t-test by hand

Formulation as a t-test using the built in R function

Graphics

Brief introduction to ggplot2

Exercise 3

Scenario 3: Paired t-test

Exercise 4

Formulation as a linear model

Formulation as a t-test by hand

Formulation as a t-test using the built in R function

Excercise

Brief introduction to `ggplot2`