Lab1: Mathematical Notation
Lab01b_Mathematical_Notation.RmdAnalysis Flowchart
One of the hardest part of Bayesian analysis is converting your idea of an ecological system from English to math or math to English.
Unlike in a lot of maximum likelihood packages, we get to decide exact how each variable in the model is defined, what distributions we think parameters come from, and what assumptions we are making about the underlying system we are trying to understand.
This process is made more confusing by the fact that we aren’t directly doing the math ourselves! We can think of the process as a fun little flow chart:
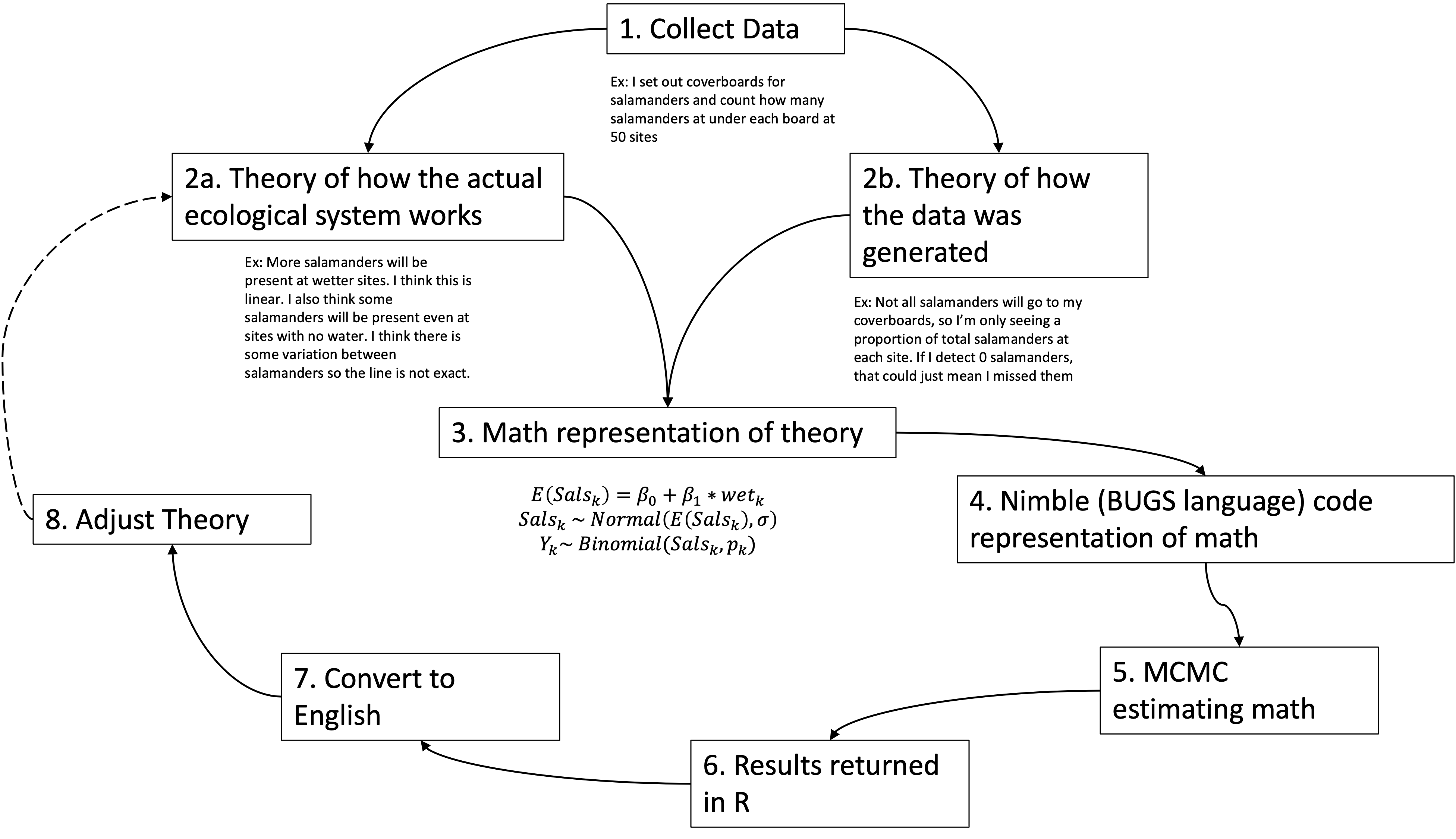
Steps 1 -3 are not specific to Bayesian analysis – you need to do the same thing for maximum likelihood analysis as well.
Also notice that steps 4 and 5 are simply how we will do Bayesian analysis in this class. You do not need MCMC software or R to perform a Bayesian analysis, it just happens to be the easiest way to do it.
A key step that will help you on your way is practicing reading math equations and translating them into English or translating them into code.
Some Useful Notation
E(x)
The expected value of something. For instance, if x is the number of frogs in a pond, E(x) is the expected number of frogs in that pond.
\phi
Phi, usually used to indicate survival probability (but can also be used willy-nilly)
Norm( \mu, \sigma^2)
The normal distribution with a mean of \mu and a standard deviation of \sigma.
Pois(\lambda)
The poisson distribution with a mean of \lambda. The poisson only accepts and produces zero or positive values
Binom(N, p)
The binomial distribution with size N and probability of success p.
\sum^w_{j=1} K_j
The sum of value K_j for values of j from 1 to w. For instance, if K_j represents the number of personalized mugs in Dr. Rushing’s office in year j , the sum of all of them from year j = 3 to year 10 would be \sum^{10}_{j=3} K_j
\beta_0 + \epsilon \sim Norm(0, \sigma^2)
A shorthand way of saying that the residuals from an equation are normally distributed. This is the assumption for most linear models and it can be quicker to write it out this way rather than as a line for E(x) and then a line for the residuals.
\beta_0 + \beta_1[q]
The value of \beta_1 depends on the value of some integer q. If q can take on 3 values (1, 2, 3), then we know there are three possible values of \beta_1. This is most commonly used for categorical variables.
logit(x) = \beta_0
This tells us x is on the probability scale (between 0 and 1) but \beta_0 is on the logit scale (all real numbers). In R, if you knew \beta_0 and wanted to get x, you would type: plogis( \beta_0 )
Math to English
You’ll often see other people’s equations in scientific papers and want to understand what they did in their analysis.
Example: Bears
I want to use data on the weight and abundance of black bears collected over the past decade to determine how bear health indices responds to different environmental and biological factors. We’re just going to focus on the Process Model - that is, how we think the system works, even if we can’t observe it directly.
We have the following information available:
| Covariate | Data Type |
|---|---|
| Time since fire | spatially and temporally varying, positive continuous |
| Percent forest cover | spatially and temporally varying, positive continuous |
| Distance to protected areas | spatially varying, positive continuous |
| Sex of Bear | binary (M = 0, F = 1) |
| Landcover | spatially and temporally varying, categorical |
| Observed weight (y) | spatially and temporally varying, positive continuous |
Let’s say I come up with the following equation. What does this mean in English?
E(weight_{it}) = \beta_0 + \beta_1*percentforest_{it} + \beta_2 * sex_i
y_{it} \sim Normal(E(weight_{it}), \sigma^2)
Answer: The expected weight of an individual bear at some time t is a function of the percent forest in the bear’s county and the sex of the bear. The observed bear weight is a normal distribution centered around with the expected weight with a standard deviation of \sigma.
What if the equation were the following?
E(weight_{it}) = \beta_0[landcover_{it}] + \beta_1*percentforest_{it} + \beta_2 * sex_i
y_{it} \sim Normal(E(weight_{it}), \sigma^2) Answer: The expected weight of an individual bear at some time t is a function of the categorical landcover, the percent forest in the bear’s county and the sex of the bear. The observed bear weight is a normal distribution centered around with the expected weight with a standard deviation of \sigma.
Example: Turtles
I’m running a headstarting experiment on spotted turtles in the Northeastern United States. All turtles were sexed before release. They were released into the wild in 3 different age groupings (juvenile, subadult, adult). I come up with the following potential model to explain the probability that each turtle i survived the 6 week study:
logit(\phi_{i}) = \phi_0[releaseage_i] + \phi_1*birthweight_i y_i \sim Bernoulli(\phi_i)
What does this mean in English?
Answer: The probability that a turtle survived the study is a function of the age group at release and the turtle’s birthweight.
Note that here y_i is going to be binary (0 = didn’t make it, 1 = survived).
Homework Questions
- Write a mathematical representation that matches the following information:
The expected weight of an individual bear at some time t is a function of the categorical landcover, the sex of the bear, and the time since fire. The relationship for time since fire is different for males and females. The observed bear weight is a normal distribution centered around with the expected weight with a standard deviation of \sigma.
Note: There are multiple ways to write this, so just choose which one makes sense to you
- Looking at the following bear equation, how would you interpret (in english) if \beta_1 were negative? How about if \beta_2 were negative?
E(weight_{it}) = \beta_0[landcover_{it}] + \beta_1*percentforest_{it} + \beta_2 * sex_i
Looking at my data again (Example 2 in Lab), I notice that we also recorded each turtle’s sex before release. Sex was recorded as either unknown, male or female. How would I add this information into the previous turtle model of survival probability? (Assume that it’s possible for turtles of each sex category to be any age.)
On a 1-10 scale, with 1 being the worst week ever and 10 being the best, how would you rate this week’s content? What lingering questions/confusion about the lecture or lab do you still have?