Lab 4: Completely randomized ANOVA

FANR 6750: Experimental Methods in Forestry and Natural Resources Research

Fall 2022

Today’s topics

  1. Brief overview of ANOVA

  2. ANOVA in R

  3. Multiple comparisons

Brief overview of ANOVA

One-way ANOVA

Scenario

  • We have independent samples from \(a > 2\) groups

  • We assume a common variance

Questions

  • Do the means differ?

  • By how much? (What are the effect sizes?)

Null hypothesis

  • \(H_0 : \mu_1 = \mu_2 = \mu_3 = . . . = \mu_a\)

  • \(H_0 : \alpha_1 = \alpha_2 = \alpha_3 = . . . = \alpha_a = 0\)

ANOVA in R

Chainshaw data

The kick angle measurements for the 4 brands of chainsaw:

library(FANR6750)
data("sawData")

head(sawData)
#>    y Brand
#> 1 42     A
#> 2 17     A
#> 3 24     A
#> 4 39     A
#> 5 43     A
#> 6 28     B

Visualize the data:

ggplot(sawData, aes(x = Brand, y = y)) +
  geom_boxplot() +
  scale_y_continuous("Kickback angle")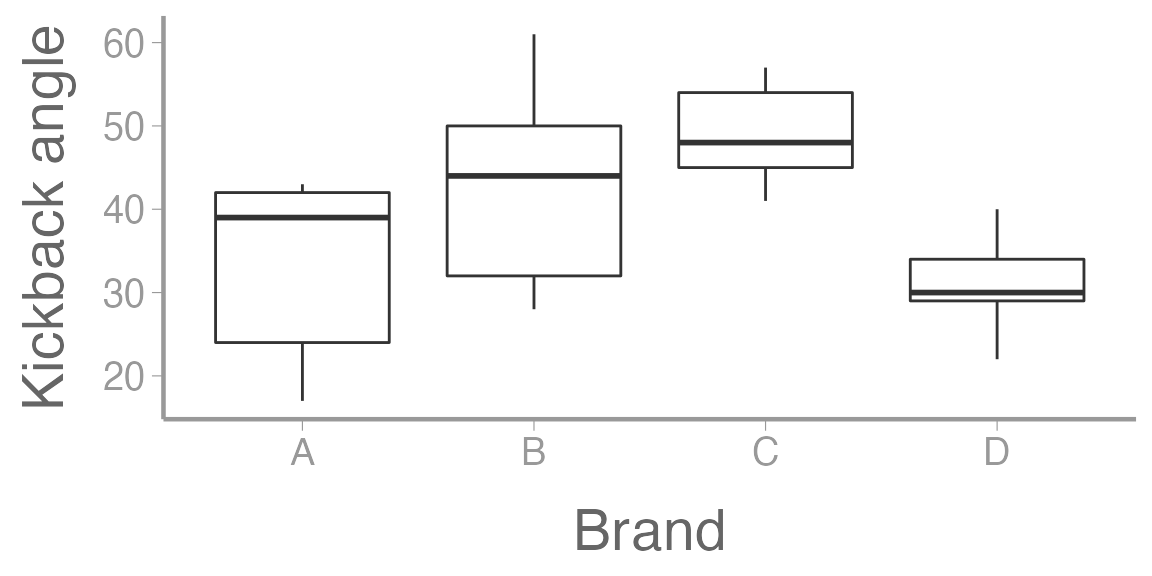

Two ANOVA function: in R: aov() and lm()

  • R has 2 common functions for doing ANOVA: aov() and lm()

  • We will primarily use aov() in this class

Crude characterization
aov() lm()
Emphasis ANOVA tables Linear models
Typical use Designed experiments Regression analysis
Multiple error strata? Yes No

Using aov()

Do the analysis 
aov.out1 <- aov(y ~ Brand, data = sawData)
View the ANOVA table 
summary(aov.out1)
#>             Df Sum Sq Mean Sq F value Pr(>F)  
#> Brand        3   1080     360    3.56  0.038 *
#> Residuals   16   1620     101                 
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The default output from summary is fine for viewing in the console but what if you want to include the ANOVA table in a report or paper? You could manually create a table and copy/paste the values, but that’s a pain. Luckily, there is a handy package called broom that turns the output from many model functions into cleaned-up data frames:

broom::tidy(aov.out1)
#> # A tibble: 2 × 6
#>   term         df sumsq meansq statistic p.value
#>   <chr>     <dbl> <dbl>  <dbl>     <dbl>   <dbl>
#> 1 Brand         3 1080.   360.      3.56  0.0382
#> 2 Residuals    16 1620    101.     NA    NA

In R Markdown, we can even include that data frame as a nicely formatted table directly in the knitted document:

aov_df <- broom::tidy(aov.out1)

options(knitr.kable.NA = '') # don't print NA's in table
knitr::kable(aov_df, 
      col.names = c("Source", "df", "SS", "MS", "F", "p"),
      align = 'c', format = "html")
Source df SS MS F p
Brand 3 1080 360.0 3.556 0.0382
Residuals 16 1620 101.2
Estimates of means ( \(\mu\)’s) and SE’s 
model.tables(aov.out1, type = "means", se = TRUE)
#> Tables of means
#> Grand mean
#>    
#> 39 
#> 
#>  Brand 
#> Brand
#>  A  B  C  D 
#> 33 43 49 31 
#> 
#> Standard errors for differences of means
#>         Brand
#>         6.364
#> replic.     5
Estimates of effect sizes ( \(\alpha\)’s) and SE’s 
model.tables(aov.out1, type = "effects", se = TRUE)
#> Tables of effects
#> 
#>  Brand 
#> Brand
#>  A  B  C  D 
#> -6  4 10 -8 
#> 
#> Standard errors of effects
#>         Brand
#>           4.5
#> replic.     5

ANOVA by hand

Grand mean 
(ybar. <- mean(sawData$y))
#> [1] 39
Group means

As with most things in R, there are several ways to calculate the group means. First, find the group means, the hard way:

A <- sawData$y[sawData$Brand == "A"]
B <- sawData$y[sawData$Brand == "B"]
C <- sawData$y[sawData$Brand == "C"]
D <- sawData$y[sawData$Brand == "D"]

(ybar.i <- c(mean(A), mean(B), mean(C), mean(D)))
#> [1] 33 43 49 31

Better yet, use tapply to find the group means (the base R way):

(ybar.i <- tapply(sawData$y, INDEX = sawData$Brand, FUN = mean))
#>  A  B  C  D 
#> 33 43 49 31

Finally, find the group means, the tidyverse way:

library(dplyr)
(ybar.i <- sawData %>% 
            group_by(Brand) %>% 
             summarise(mu = mean(y)))
#> # A tibble: 4 × 2
#>   Brand    mu
#>   <chr> <dbl>
#> 1 A        33
#> 2 B        43
#> 3 C        49
#> 4 D        31

Although each of these methods does what we want - return the mean kickback angle for each group - note that they do not return the same type of object.

Use the class() function to see what type of object each one returns.

When might the output from each method be useful?

Sum of squares

Sums of squares among

# Number of saw brands
a <- length(unique(sawData$Brand))

# Number of measurements of each brand (note, this assumes balanced design)
n <- nrow(sawData)/a

SSa <- n * sum((ybar.i$mu - ybar.)^2)
SSa
#> [1] 1080

Sums of squares within

# individual saw data
y.ij <- sawData$y

SSw <- sum((y.ij - rep(ybar.i$mu, each = n)) ^ 2)
SSw
#> [1] 1620
Means squares

Mean squares among

df1 <- a - 1
(MSa <- SSa / df1)
#> [1] 360

Mean squares within

df2 <- a * (n - 1)
(MSw <- SSw / df2)
#> [1] 101.2
F-statistic 
(F.stat <- MSa / MSw)
#> [1] 3.556
Critical values and p-values

Recall that in ANOVA, we only consider the upper tail of the F-distribution.

Critical value:

alpha <- 0.05
(F.crit <- qf(1 - alpha, df1, df2))
#> [1] 3.239

p-value

(p.value <- 1 - pf(F.stat, df1, df2))
#> [1] 0.03823

Multiple comparisons

Group means +1 SE 
mean.SE <- 6.364 # from model.tables() -- see slide 7.

# Add SE column
ybar.i <- dplyr::mutate(ybar.i, SE = mu + mean.SE)

ggplot(ybar.i, aes(x = Brand, y = mu, fill = Brand)) +
  geom_col() +
  geom_errorbar(aes(ymin = mu, ymax = SE), width = 0) +
  scale_y_continuous("Chainsaw kickback angle")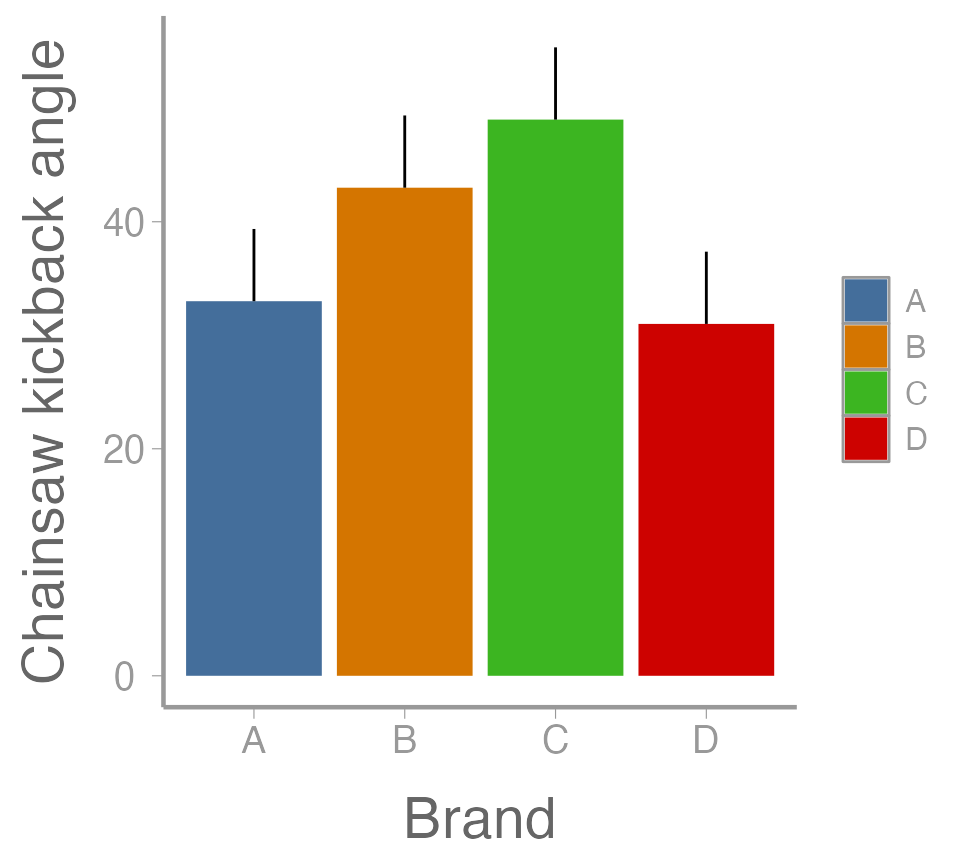

Tukey’s Honestly Significant Difference test 

TukeyHSD(aov.out1)
#>   Tukey multiple comparisons of means
#>     95% family-wise confidence level
#> 
#> Fit: aov(formula = y ~ Brand, data = sawData)
#> 
#> $Brand
#>     diff     lwr     upr  p adj
#> B-A   10  -8.207 28.2074 0.4214
#> C-A   16  -2.207 34.2074 0.0956
#> D-A   -2 -20.207 16.2074 0.9888
#> C-B    6 -12.207 24.2074 0.7826
#> D-B  -12 -30.207  6.2074 0.2727
#> D-C  -18 -36.207  0.2074 0.0532
Plot Tukey’s confidence intervals 
plot(TukeyHSD(aov.out1))

Assignment

A biologist wants to compare the growth of four different tree species she is considering for use in reforestation efforts. All 32 seedlings of the four species are planted at the same time in a large plot. Heights in meters recorded after several years.

Create an R Markdown file to do the following:

  1. Create an R chunk to load the data using:
library(FANR6750)
data("treeHt")

  1. Create a header called “Hypotheses” and under this header, indicate, in plain English, what the null and alternative hypotheses are. Also use R Markdown’s equation features to write these hypotheses (to the extent possible) using mathematical notation

  2. Create a header called “ANOVA by hand”. Under this header, perform an ANOVA analysis (degrees of freedom, sums-of-squares, mean-squares, and F-value) without using aov(). Compute either the critical value of F, or the p-value. Be sure to annotate your code.

  3. Create a header called “ANOVA in R”. Under this header, perform an ANOVA analysis on the data using the aov() function

  4. Under a subheader called “ANOVA results”:

    • indicate whether or not the null hypothesis can be rejected at the \(\alpha = 0.05\) level

    • include a well-formatted ANOVA table using the broom::tidy() function

    • create a barplot showing the group means and SEs

  5. Create a header called “Which means are different?”. Use Tukey’s HSD test to determine which pairs of means differ at the \(\alpha = 0.05\) level. Include a few sentences indicating which pairs are different

A few things to remember when creating the assignment:

  • Be sure the output type is set to: output: html_document

  • Title the document: title: "Homework 1"

  • Be sure to include your first and last name in the author section

  • Be sure to set echo = TRUE in all R chunks so we can see both your code and the output

  • Please upload both the html and .Rmd files when you submit your assignment

  • See the R Markdown reference sheet for help with creating R chunks, equations, tables, etc.