Lab 7: Randomized Complete Block Design

Recap

Remember from lecture that randomized complete block design (RCBD) is like one-way ANOVA except experimental units are organized into blocks to account for extraneous source of variation.

Blocks can be regions, time periods, individual subjects, etc. but blocking must occur during the design phase of the study.

We can write the additive RCBD model as:

\[\large y_{ij} = \mu + \alpha_i + \beta_j + \epsilon_{ij}\]

Blocked ANOVA by hand

To “fit” the RCBD model by hand, we’ll use the gypsy moth data we saw in lecture:

library(FANR6750)
data("mothData")

head(mothData)

Treatment	Region	caterpillar
Control	1	25
Control	2	10
Control	3	15
Control	4	32
Bt	1	16
Bt	2	3

Factors

So far, we have generally treated data as either numeric/integer if the vector consisted of numbers, or character if the data consisted of non-numeric information. To perform the RCBD analysis, we need to learn about another type of object in R - factors.

Factors look like character strings but they behave quite differently, and understanding the way that R handles factors is key to working this type of data. The key difference between factors and character strings is that factors are used to represent categorical data with a fixed number of possible values, called levels¹.

Factors can be created using the factor() function:

age <- factor(c("adult", "juvenile", "adult", "juvenile"))

Because we didn’t explicitly tell R the levels of this factor, it will assume the levels are adult and juvenile. Furthermore, by default R assigns levels in alphabetical order, so adult will be the first level and juvenile will be the second level:

levels(age)
#> [1] "adult"    "juvenile"

Sometimes alphabetical order might not make sense:

treatment <- factor(c("medium", "low", "high"))

What order will R assign to the treatment levels?

If you want to order the factor in a different way, you can use the optional levels argument:

treatment <- factor(c("low", "medium", "high"), levels = c("low", "medium", "high"))
levels(treatment)
#> [1] "low"    "medium" "high"

Sometimes you may also need to remove factor levels. For example, let’s see what happens if we have a type in one of the factors:

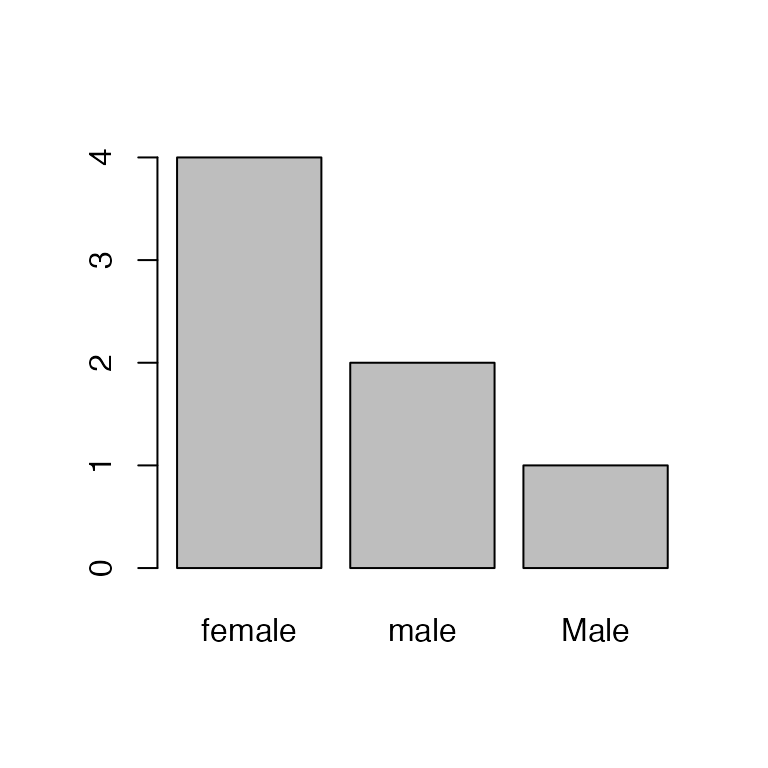
sex = factor(c("male", "female", "female", "Male", "male", "female", "female"))

barplot(table(sex))

Oops, one of the field techs accidentally capitalized “Male”. Let’s change that to lowercase:

sex[sex == "Male"] <- "male"
barplot(table(sex))

Hmm, there’s still a bar for Male. We can see what’s happening here by looking at the levels:

levels(sex)
#> [1] "female" "male"   "Male"

Removing/editing the factors doesn’t change the levels! So R still thinks there are three levels, just zero Male entries. To remove that mis-specified level, we need to drop it:

sex <- droplevels(sex)
barplot(table(sex))

That’s better.

The bottom line is be careful when working with factors, since their behavior is not always intuitive. There are more great online resources for working with factors in R, including this tutorial and even a package (forcats) that tries to make it a bit easier.

Back to the data

Before we analyze the moth data, we need to tell R to treat the Treatment and Plot variables as factors:

str(mothData)
#> 'data.frame':    12 obs. of  3 variables:
#>  $ Treatment  : chr  "Control" "Control" "Control" "Control" ...
#>  $ Region     : int  1 2 3 4 1 2 3 4 1 2 ...
#>  $ caterpillar: num  25 10 15 32 16 3 10 18 14 2 ...

Right now, they are character and integer objects, respectively.

mothData$Treatment <- factor(mothData$Treatment, levels = c("Control", "Bt", "Dimilin"))
levels(mothData$Treatment)
#> [1] "Control" "Bt"      "Dimilin"

mothData$Region <- factor(mothData$Region)
levels(mothData$Region)
#> [1] "1" "2" "3" "4"

Note that we were explicit about the order of levels for Treatment so that controls came first.

Means

Next, compute the means:

library(dplyr)

# Grand mean
(grand.mean <- mean(mothData$caterpillar))
#> [1] 14.42

# Treatment means
(treatment.means <- group_by(mothData, Treatment) %>% summarise(mu = mean(caterpillar)))
#> # A tibble: 3 × 2
#>   Treatment    mu
#>   <fct>     <dbl>
#> 1 Control    20.5
#> 2 Bt         11.8
#> 3 Dimilin    11

# Block means
(block.means <- group_by(mothData, Region) %>% summarise(mu = mean(caterpillar)))
#> # A tibble: 4 × 2
#>   Region    mu
#>   <fct>  <dbl>
#> 1 1       18.3
#> 2 2        5  
#> 3 3       13.7
#> 4 4       20.7

Treatment sums of squares

Remember the formula for the treatment sums of squares

\[\Large b \times \sum_{i=1}^a (\bar{y}_i - \bar{y}_.)^2\]

b <- nlevels(mothData$Region)
(SS.treat <- b * sum((treatment.means$mu - grand.mean)^2))
#> [1] 223.2

Block sums of squares

The formula for the block sums of squares

\[\Large a \times \sum_{j=1}^b (\bar{y}_j - \bar{y}_.)^2\]

a <- nlevels(mothData$Treatment)
(SS.block <- a * sum((block.means$mu - grand.mean)^2))
#> [1] 430.9

Within groups sums of squares

\[\Large \sum_{i=1}^a \sum_{j=1}^b (y_{ij} - \bar{y}_i - \bar{y}_j + \bar{y}_.)^2\]

treatment.means.long <- rep(treatment.means$mu, each = b)
block.means.long <- rep(block.means$mu, times = a)
(SS.within <- sum((mothData$caterpillar - treatment.means.long - block.means.long + grand.mean)^2))
#> [1] 114.8

NOTE: For the above code to work, treatment.means and block.means must be in the same order as in the original data.

Create ANOVA table

Now we’re ready to create the ANOVA table. Start with what we’ve calculated so far:

df.treat <- a - 1
df.block <- b - 1
df.within <- df.treat*df.block
ANOVAtable <- data.frame(df = c(df.treat, df.block, df.within),
                         SS = c(SS.treat, SS.block, SS.within))
rownames(ANOVAtable) <- c("Treatment", "Block", "Within")
ANOVAtable
#>           df    SS
#> Treatment  2 223.2
#> Block      3 430.9
#> Within     6 114.8

Next, add the mean squares:

MSE <- ANOVAtable$SS / ANOVAtable$df
ANOVAtable$MSE <- MSE ## makes a new column!

Now, the F-values (with NA for error/within/residual row):

F.stat <- c(MSE[1]/MSE[3], MSE[2]/MSE[3], NA)
ANOVAtable$F.stat <- F.stat

Finally, the p-values

p <- c(1 - pf(F.stat[1], 2, 6), 1 - pf(F.stat[2], 3, 6), NA)
ANOVAtable$p <- p

Quick reminder about calculating p-values

qf(0.95, 2, 6) # 95% of the distribution is below this value of F
#> [1] 5.143

1-pf(F.stat[1], 2, 6) # Proportion of the distribution beyond this F value
#> [1] 0.03922

Be sure you understand what each of these functions is doing!

And we’ll display the table using kable(), with a few options to make it look a little nicer:

options(knitr.kable.NA = "") # leave NA cells empty
knitr::kable(ANOVAtable, digits = 2, align = "c",
             col.names = c("df", "SS", "MSE", "F", "p-value"),
             caption = "RCBD ANOVA table calculated by hand")

RCBD ANOVA table calculated by hand
	df	SS	MSE	F	p-value
Treatment	2	223.2	111.58	5.83	0.04
Block	3	430.9	143.64	7.51	0.02
Within	6	114.8	19.14

Blocked ANOVA using `aov()`

aov1 <- aov(caterpillar ~ Treatment + Region, mothData)
summary(aov1)
#>             Df Sum Sq Mean Sq F value Pr(>F)  
#> Treatment    2    223   111.6    5.83  0.039 *
#> Region       3    431   143.6    7.51  0.019 *
#> Residuals    6    115    19.1                 
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Same as what we got by hand! Look what happens if we ignore the blocking variable:

aov2 <- aov(caterpillar ~ Treatment, mothData)
summary(aov2)
#>             Df Sum Sq Mean Sq F value Pr(>F)
#> Treatment    2    223   111.6    1.84   0.21
#> Residuals    9    546    60.6

Why is the effect of pesticide no longer significant?

Treating block effects as random effects

aov3 <- aov(caterpillar ~ Treatment + Error(Region), mothData)
summary(aov3)
#> 
#> Error: Region
#>           Df Sum Sq Mean Sq F value Pr(>F)
#> Residuals  3    431     144               
#> 
#> Error: Within
#>           Df Sum Sq Mean Sq F value Pr(>F)  
#> Treatment  2    223   111.6    5.83  0.039 *
#> Residuals  6    115    19.1                 
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The values of the ANOVA table are the same as before, and there is no reason to use random effects here if interest only lies in testing the null hypothesis concerning pesticides.

Later, we will see cases where it is important to use random and fixed effects.

Assignment (not for a grade)

Some time ago, plantations of Pinus caribaea were established at four locations on Puerto Rico. As part of a spacing study, four spacings were used at each location to determine the effect of four specific spacing intervals on tree height. Twenty years after the plantations were established, measurements were made in the study plots as follows:

Location	Spacing (ft)	Height (ft)
Caracoles	5	72
	7	80
	10	85
	14	91
Utuado	5	75
	7	90
	10	94
	14	112
Guzman	5	88
	7	95
	10	94
	14	91
Lares	5	79
	7	94
	10	104
	14	106

You can access these data using:

library(FANR6750)
data("pineData")

Questions/tasks

What is the primary null hypothesis of interest? State it, and the associated alternative hypothesis, as comments in the file
Test for effects of location and spacing on plant height using the aov() function. NOTE: spacing must be treated as a factor, not as a numeric vector
Perform a Tukey test to determine which spacings differ

Put your answers in an R Markdown report. Your report should include:

A well-formatted ANOVA table (with caption); and
A publication-quality plot (or plots) of the estimated effect of location and spacing on plant height. The figure(s) should also have a descriptive caption and any aesthetics (color, line type, etc.) should be clearly defined.

You may format the report however you like but it should be well-organized, with relevant headers, plain text, and the elements described above.

As always:

Be sure the output type is set to: output: html_document
Be sure to set echo = TRUE in all R chunks
See the R Markdown reference sheet for help with creating R chunks, equations, tables, etc.
See the “Creating publication-quality graphics” reference sheet for tips on formatting figures

Under the hood, R actually treats factors as integers - 1, 2, 3… - with character labels for each level↩︎

FANR 6750: Experimental Methods in Forestry and Natural Resources Research

Fall 2022

Recap

Blocked ANOVA by hand

Factors

Back to the data

Means

Treatment sums of squares

Block sums of squares

Within groups sums of squares

Create ANOVA table

Blocked ANOVA using `aov()`

Treating block effects as random effects

Assignment (not for a grade)

Lab 7: Randomized Complete Block Design

FANR 6750: Experimental Methods in Forestry and Natural Resources Research

Fall 2022

Recap

Blocked ANOVA by hand

Factors

Back to the data

Means

Treatment sums of squares

Block sums of squares

Within groups sums of squares

Create ANOVA table

Blocked ANOVA using aov()

Treating block effects as random effects

Assignment (not for a grade)

Blocked ANOVA using `aov()`