Lab 14: Model selection and multimodel inference

FANR 6750: Experimental Methods in Forestry and Natural Resources Research

Fall 2021

Overview

  1. Model fitting

  2. Model selection

  3. Multi-model inference

Model fitting

We will start by fitting several alternative models to explain avian richness across Switzerland:

library(FANR6750)
data("swissData")
head(swissData)
elevation forest water sppRichness
450 3 No 35
450 21 No 51
1050 32 No 46
950 9 Yes 31
1150 35 Yes 50
550 2 No 43

The four linear models contain different combinations of forest cover, elevation, and water:

fm1 <- lm(sppRichness ~ forest, data = swissData)
fm2 <- lm(sppRichness ~ elevation, data = swissData)
fm3 <- lm(sppRichness ~ forest + elevation + water, data = swissData)
fm4 <- lm(sppRichness ~ forest + elevation + I(elevation^2) + water, data = swissData)

Critically, all four of these models represent plausible hypotheses about factors that influence avian richness. We have no a priori knowledge of which model might be a better explanation for observed patterns.

Let’s look for closely at the output from model 4:

summary(fm4)
#> 
#> Call:
#> lm(formula = sppRichness ~ forest + elevation + I(elevation^2) + 
#>     water, data = swissData)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -11.314  -3.205  -0.377   3.334  15.083 
#> 
#> Coefficients:
#>                 Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)     4.52e+01   1.29e+00   35.14  < 2e-16 ***
#> forest          2.31e-01   1.28e-02   18.11  < 2e-16 ***
#> elevation      -1.02e-02   2.57e-03   -3.95   0.0001 ***
#> I(elevation^2)  6.10e-08   9.66e-07    0.06   0.9497    
#> waterYes       -3.01e+00   6.82e-01   -4.42  1.5e-05 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 4.95 on 262 degrees of freedom
#> Multiple R-squared:  0.793,  Adjusted R-squared:  0.79 
#> F-statistic:  251 on 4 and 262 DF,  p-value: <2e-16

What does each parameter represent?

summary.aov(fm4)
#>                 Df Sum Sq Mean Sq F value  Pr(>F)    
#> forest           1  13311   13311  542.40 < 2e-16 ***
#> elevation        1  10820   10820  440.89 < 2e-16 ***
#> I(elevation^2)   1      7       7    0.27     0.6    
#> water            1    479     479   19.52 1.5e-05 ***
#> Residuals      262   6430      25                    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Using the ANOVA table, we could compute AIC using the equation \(AIC = n \log(RSS/n) + 2K\), where RSS is the residual sum-of-squares. However, we will use the more general formula: \(AIC = −2L(\hat{\theta}; y) + 2K\).

Model selection

First, let’s calculate AIC by hand:

# Sample size
n <- nrow(swissData)

# Log-likelihood for each model
logL <- c(logLik(fm1), logLik(fm2), logLik(fm3), logLik(fm4))

# Number of parameters
K <- c(3, 3, 5, 6)

# AIC
AIC <- -2 * logL + 2 * K

# delta AIC
delta <- AIC - min(AIC)

#AIC Weights
w <- exp(-0.5 * delta)/sum(exp(-0.5 * delta))

And now we can create the AIC table:

# Put vectors in data.frame
ms <- data.frame(logL, K, AIC, delta, w)
rownames(ms) <- c("fm1", "fm2", "fm3", "fm4")
ms <- dplyr::arrange(ms, -w) # arrange by descending weight
kable(ms, digits = 2)
logL K AIC delta w
fm3 -803.6 5 1617 0.0 0.73
fm4 -803.6 6 1619 2.0 0.27
fm2 -934.1 3 1874 257.0 0.00
fm1 -939.0 3 1884 266.9 0.00

Just to check our results, we can do the same thing using R’s built-in AIC() function:

ms2 <- AIC(fm1, fm2, fm3, fm4)
ms2 <- dplyr::arrange(ms2, AIC) # arrange by AIC
kable(ms2)
df AIC
fm3 5 1617
fm4 6 1619
fm2 3 1874
fm1 3 1884

Note that ff we had used the residual sums-of-squares instead of the log-likelihoods, the AIC values would have been different, but the \(\Delta\)AIC values would have been the same. Either approach is fine with linear models, but log-likelihoods must be used with GLMs and other models fit using maximum likelihood

Multi-model inference

Based on AIC scores, model 3 appears to be the “best” model but there’s also reasonable support for other models. What if we want to predict avian richness using all of the models? Why might we want to do this?

First, let’s estimate the expected number of species at 1000m elevation, 25% forest cover, and no water, for each model:

(predData1 <- data.frame(elevation = 1000, 
                         forest = 25, 
                         water = "No"))
#>   elevation forest water
#> 1      1000     25    No

E1 <- predict(fm1, newdata = predData1, type = "response")
as.numeric(E1) # remove names (optional)
#> [1] 37.9

E2 <- predict(fm2, newdata = predData1, type = "response")
as.numeric(E2)
#> [1] 42.53

E3 <- predict(fm3, newdata = predData1, type = "response")
as.numeric(E3)
#> [1] 40.89

E4 <- predict(fm4, newdata = predData1, type = "response")
as.numeric(E4)
#> [1] 40.86

What is the expected number of species at 1000m, 25% forest cover, and no water, averaged over all 4 models?

E1 * w[1] + E2 * w[2] + E3 * w[3] + E4 * w[4]
#>     1 
#> 40.88

What if we want to predict species richness over range of forest cover? First, the predictions for each model:

predData2 <- data.frame(forest = seq(0, 100, length = 50), 
                        elevation = 1000, 
                        water = "No")
E1 <- predict(fm1, newdata = predData2)
E2 <- predict(fm2, newdata = predData2)
E3 <- predict(fm3, newdata = predData2)
E4 <- predict(fm4, newdata = predData2)

Emat <- cbind(E1, E2, E3, E4)

How do we model-average these vectors?

Eavg <- Emat %*% w

Be sure you understand what R is doing here and how it results in the appropriate predictions.

And plot the predictions from each model and the model averaged results. First we need to combine the predictions into a single data frame. Then we’ll use some creative (and perhaps not every effective) sizing so that we can see the overlapping predictions from models 3, 4, and the model-averaged results:

library(ggplot2)

predDF <- data.frame(pred = c(Eavg, E1, E2, E3, E4),
                     Model = rep(c("Model average", "Model 1", "Model 2", "Model 3", "Model 4"),
                                 each = length(E1)),
                     forest = rep(predData2$forest, 5))

predDF$Model <- factor(predDF$Model, 
                       levels = c("Model average", "Model 4", "Model 3", "Model 2", "Model 1"))
ggplot() +
  geom_point(data = swissData, aes(x = forest, y = sppRichness), alpha = 0.4) +
  geom_line(data = predDF, aes(x = forest, y = pred, color = Model, size = Model)) +
  scale_size_manual(values = c(5, 2, 0.5, 0.5, 0.5)) +
  scale_x_continuous("Forest cover") +
  scale_y_continuous("Species richness")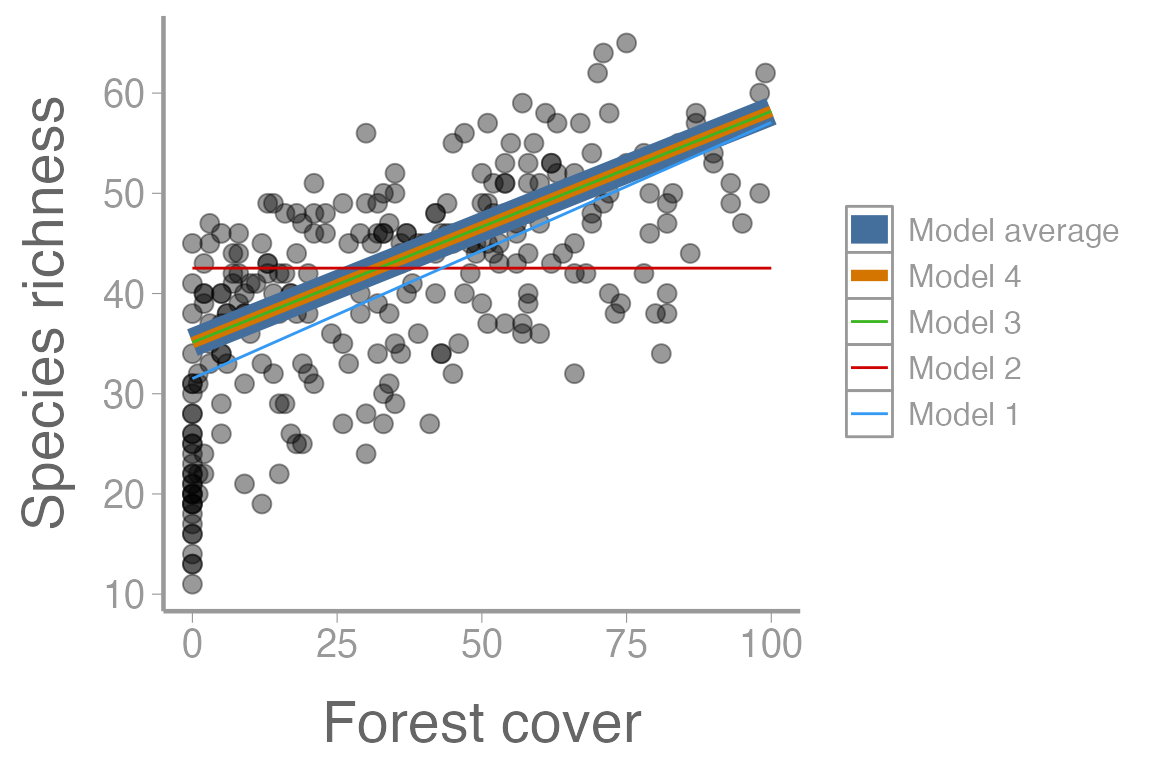

Assignment (not to be turned in!)

Create an R markdown report, using the jayData from lab 12, to do the following:

  1. Fit four linear models of jay abundance. Include elevation all four models. Include at least one interaction, and one quadratic term for elevation.

  2. Create AIC table by hand, not using R’s AIC function

  3. Model-average regression lines of jay abundance and elevation. Plot the averaged regression line along with the regression lines from each model.

  4. Bonus: Create a map showing the model-averaged estimates of jay abundance on Santa Cruz Island. (Hint: use predict() with cruzData supplied as the newdata argument)

As always:

  • Be sure the output type is set to: output: html_document

  • Title the document: title: "Lab 14 assignment"

  • Be sure to include your first and last name in the author section

  • Be sure to set echo = TRUE in all R chunks so we can see both your code and the output

  • Please upload both the html and .Rmd files when you submit your assignment

  • See the R Markdown reference sheet for help with creating R chunks, equations, tables, etc.